
[데이터통신] 3. 데이터와 신호
이전 글 : [데이터통신] 2. 네트워크와 모델 [데이터통신] 2. 네트워크와 모델 이전 글 : [데이터통신] 1. 데이터 통신의 개요 [데이터통신] 1. 데이터 통신의 개요 [1] 데이터 통신 * 데이터 통신 : 전
heynary.tistory.com
[1] 디지털-대-디지털 변환
- 회선 부호화 (Line Coding) : 디지털 데이터를 디지털 신호로 변환
- 블록 부호화 (Block Coding) / 뒤섞기 (Scrambling) : 경우에 따라 필요한 작업
* 데이터 요소 : 데이터를 나타내는 가장 작은 단위체, 비츠
* 신호 요소 : 신호의 가장 짧은 단위
* N, 데이터전송율 (data rate) = 비트율 (bit rate) : 1초당 전송된 데이터요소의 개수 [bps]
* S, 신호 전송율 (signal rate) = 펄스율 = 변조율 : 1초당 전송된 신호 요소의 개수 [baud rate, 보울]
- r : 매 신호요소 당 전송되는 데이터요소의 개수
- C : 경우요인 (데이터 패턴에 따른 신호율의 변화)
* 대역폭 : 비주기 디지털신호의 이론적 대역폭은 무한대이지만, 실제 유효한 대역폭은 유한함
- 진폭이 작은 부분은 무시
- 비트율이 아닌, 보울이 디지털 신호의 요구 대역폭을 결정함 : 신호전송율이 중요!
- 특정 전송율을 제공하기 위한 최소 대역폭
- 채널의 대역폭이 주어질 때 최대 전송율 : 나이퀴스트 공식과의 관계
* 회선부호화 방식

- NRZ/I : B=N/2 의 작은 신호율을 가지나, 연속적인 0 비트로 동기화 문제가 발생할 수 있음
- 양위상 (Bipolar) 맨체스터 : 동기화와 비트 표현을 위해 비트 중간 지점에서 신호를 반전시킴.
-> 양-대-음 : 비트0, 음-대-양 : 비트1
-> 차분 맨체스터 부호화 방식 : 비트 시작점에 변화가 있으면 비트0, 변화가 없으면 비트1
-> 항상 비트 중간에 신호가 반전되어 직류성분이 없고 동기화 가능
-> 신호율이 증가하는 단점이 있음, r=1/2
* 블록부호화 방식 : 원본데이터 외에 추가적인 비트정보를 포함 (동기화 정보, 오류탐지 정보)
- 4B/5B (4Binary/5Binary) : 4비트 데이터를 5비트 데이터로 바꾸며 NRZ/I 때 발생하는 연속적인 0의 비트로 인한 문제가 발생하지 않게 한다. 25%의 보오율 증가가 발생한다.
예제. 1Mbps 의 속도로 데이터를 전송해야 한다 . 4B/5B 와 NRZ -I를 조합하여 사용하는 경우와 맨체스터 부호화를 사용하는 경우의 최소 요구 대역폭은 얼마인가 ?
풀이.
4B/5B 적용 시, 25% 보오율 증가로 인해 1.25Mbps로 증가한다.
NRD-I 적용 시, 최소 요구대역폭 = N/2 = 625kHz
맨체스터 부호화 사용 시, 최소 요구대역폭=N=1MHz 로 더 넓은 대역폭을 요구하나, 직류성분의 문제가 없다.
[2] 아날로그-대-디지털 변환
* 펄스 코드 변조 (PCM, Pulse Code Modulation = PAM, Pulse Amplitude Modulation) : 채집 (sampling)
- 아날로그 데이터를 Ts마다 채집 (채집 시 아직 아날로그 값임)
- Ts : 채집기간 (주기)
- fs : 채집 주파수
* 표본 채집율 (Sampling rate) : 나이퀴스트 정리에 의해, 채집율은 신호에 포함된 최대 주파수의 최소 2배임.
예제1. 사람의 음성은 최대 4000Hz 의 주파수를 갖는다 . 어느 정도의 채집율을 사용해야 하나 ?
fs= 2 X 4000 Hz = 8000 Hz
예제2. 어떤 복잡한 띠대역 통과 신호의 대역폭이 200kHz이다 . 이 신호의 최소 채집율은 얼마인가 ?
주파수와 최대 주파수값을 모르기 때문에 , 최소 채집율을 알 수 없음.
나이퀴스트 정리에 의해, 채집율은 신호에 포함된 최대 주파수의 최소 2배임.
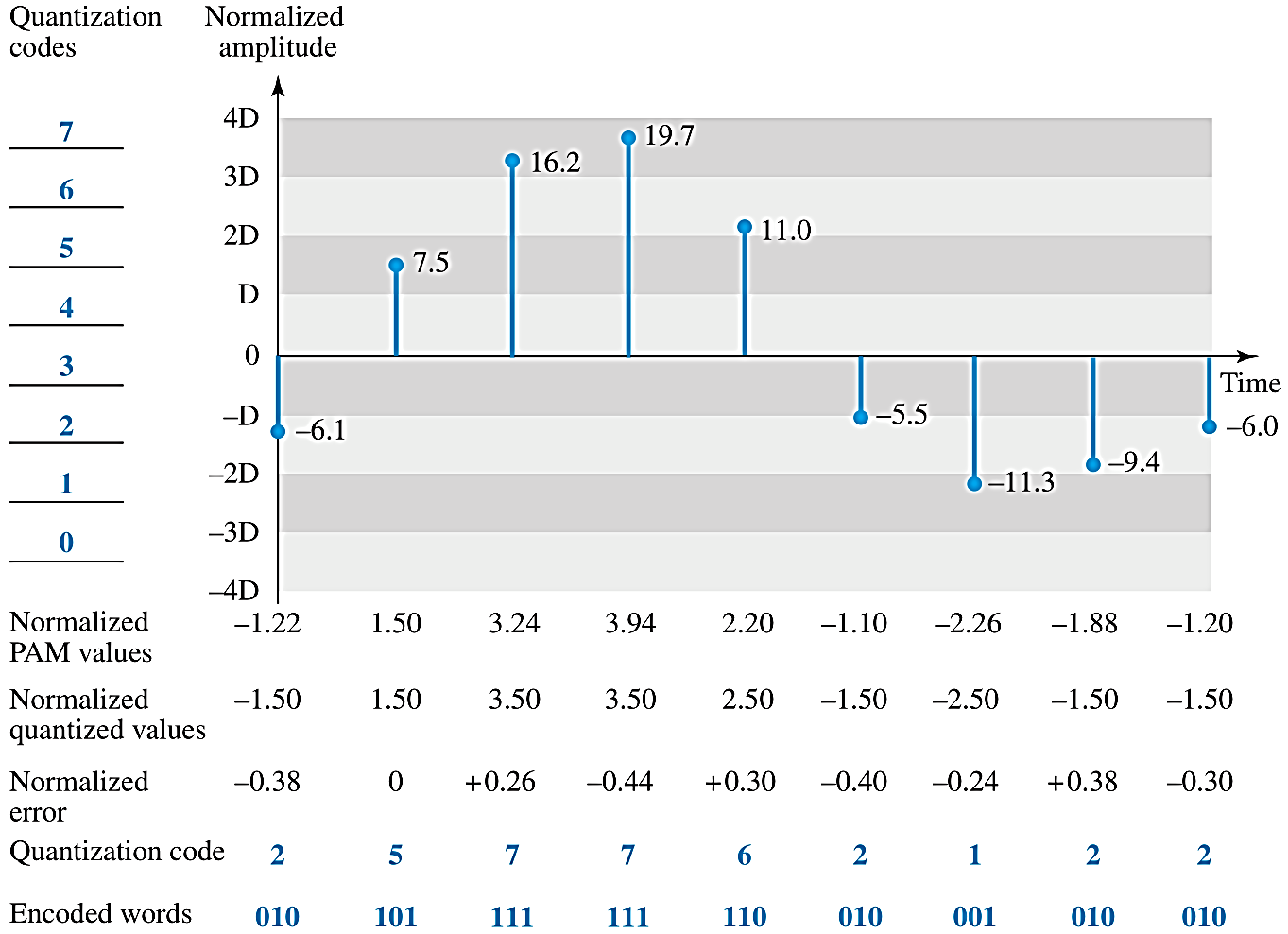
* 계수화 (=양자화, quantization) : 아날로그 데이터는 Vmax, Vmin 사이의 진폭값을 가질 때 전체 영역을 높이의 L개 구간으로 나눔
- 각 구간의 중간점에 0부터 (L-1)까지 계수화된 값을 지정함
- 채집된 신호의 진폭값을 계수화된 값의 하나로 근사화해 지정
- L이 너무 작으면, 계수화 오차가 커짐
- L이 너무 커지면, 계수화 오차는 감소하나 최종 디지털 데이터양이 너무 커짐
* 계수화 오차 (=양자화 오차) : 아날로그 데이터를 디지털 데이터로 근사화하는 과정에서 발생하는 오차
−Δ/𝟐 ≤ (quantizationerror)≤ Δ/𝟐
* 부호화 (Encoding) : 채집된 표본들이 계수화되고 표본당 비트수가 정해진 후 각 표본들이 𝒏𝒃 비트의 부호로 바뀌는 것
- 최종 디지털 데이터의 비트율
(Bit rate)=(Sampling rate)×(Number of bits per sample)
=𝒇𝒔×𝒏𝒃
예제. 사람의 목소리는 보통 0에서 4000Hz 사이의 주파수를 갖는다 .이것을 표본당 8비트의 디지털 데이터로 변환하면 비트율은 얼마인가 ?
풀이.
표본 채집율 fs= 4000 X 2 = 8000 Hz
(Bit rate)=(Sampling rate)×(Number of bits per sample)
표본 채집율 X 표본당 비트수 = 8000 X 8 = 64,000 bits/sec = 64 kbps
'ELECTRONIC ELECTRICAL ENG > 정보통신 & IT' 카테고리의 다른 글
| [데이터통신] 6. 대역폭 활용 (0) | 2022.06.05 |
|---|---|
| [데이터통신] 5. 아날로그 전송 (0) | 2022.06.05 |
| [데이터통신] 3. 데이터와 신호 (2) | 2022.06.05 |
| [데이터통신] 2. 네트워크와 모델 (0) | 2022.06.04 |
| [데이터통신] 1. 데이터 통신의 개요 (0) | 2022.06.04 |




댓글